№ 11.15 Геометрія = № 23.15 Математика
Тупий кут прямокутної трапеції дорівнює 120°, а менша діагональ трапеції дорівнює більшій бічній стороні. Знайдіть відношення середньої лінії трапеції до більшої бічної сторони.
Розв'язок:
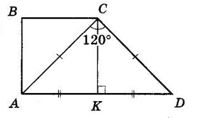
Проведемо CK ⊥ AD.
За умовою ΔACD рівнобедрений, AC = CD.
Тоді CK — висота і медіана:
AK = KD.
ΔBCK — прямокутник, BC = AK.
Нехай BC = x,
тоді AD = 2AK = 2x.
Середня лінія:
$\frac{BC\ +\ AD}{2}=\ \frac{x\ +\ 2x}{2}\ =\ \frac{3x}{2}.$
У ΔCKD ∠DCK = 120° − 90° = 30°,
тоді KD = $\frac{1}{2}$ CD (катет проти кута 30°).
CD = 2KD = 2x.
Відношення середньої лінії до більшої бічної сторони:
$\frac{3x}{2}: 2x = 3x∶ 4x = 3∶ 4.$
Відповідь:
3 : 4.
