ВПР 1 №84 Геометрія = ВПТ 4 №43 Математика
У рівнобічній трапеції більша основа дорівнює a см, бічна сторона – c см, а гострий кут – 60°. Знайдіть середню лінію трапеції.
Розв'язок:
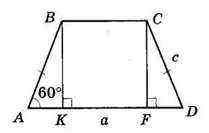
Проведемо BK ⊥ AD, CF ⊥ AD — висоти трапеції.
У ΔABK ∠ABK = 90° − ∠BAK =
= 90° − 60° = 30°.
Тоді AK = $\frac{1}{2}$ AB = $\frac{c}{2}$ (як катет, що лежить проти кута 30°).
BK || CF (BK ⊥ AD, CF ⊥ AD) BK = CF за гіпотенузою і гострим кутом (AB = CD, ∠A = ∠D за умовою).
Тоді KBCF — паралелограм.
BC = KF = AD − (AK + FD) =
= a − $2\frac{c}{2}$ = a – c.
Середня лінія: $\frac{AD + BC}{2}$ =
= $\frac{a + a – c}{2}$ = $\frac{2a – c}{2}$ = a – $\frac{c}{2}$.
Відповідь:
a – $\frac{c}{2}$.
