Завдання № 75

ВПР 1 №75 Геометрія =  ВПТ 4 №34 Математика

Послідовно сполучили середини сторін квадрата, діагональ якого дорівнює d см. Визначте вид чотирикутника, що при цьому утворився, та обчисліть його периметр.

Розв'язок:

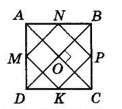
ABCD — квадрат, M, N, P, K — середини його сторін.  
AC = BD = d — діагоналі квадрата.
У ΔABC NP — середня лінія, NP || AC, NP = $\frac{1}{2}$ AC = $\frac{d}{2}$.  
У ΔADC MK — середня лінія, MK || AC, MK = $\frac{1}{2}$ AC = $\frac{d}{2}$.  
Дві протилежні сторони чотирикутника MNPK паралельні і рівні.
MNPK — паралелограм.
Аналогічно, MN || BD, MN = $\frac{1}{2}$ BD = $\frac{d}{2}$.
KP || BD, KP = $\frac{1}{2}$ BD = $\frac{d}{2}$. Отже, MNPK — ромб.  
MN ⊥ MK (MN || BD, MK || AC, BD ⊥ AC), тоді MNPK — квадрат.  
P_MNPK = $4\frac{d}{2}$ = 2d (см).

Відповідь:

квадрат.