ВПР 1 №6 Геометрія = ВПТ 2 №6 Математика
Усі сторони чотирикутника між собою рівні. Доведіть, що сума будь−яких двох сусідніх кутів цього чотирикутника дорівнює 180°.
Розв'язок:
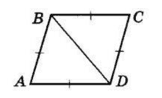
ABCD — чотирикутник, AB = BC = CD = AD.
Проводимо діагональ BD. ΔABD = ΔCBD за трьома сторонами.
З рівності трикутників ∠ABD = ∠CDB.
У ΔABD ∠A + ∠ABD + ∠ADB = 180°,
∠A + ∠CDB + ∠ADB = 180°,
∠A + ∠ADC = 180°.
Аналогічно можна довести, що сума інших пар сусідніх кутів теж дорівнює 180°.
