ВПР 1 №41 Геометрія = ВПТ 2 №41 Математика
У квадрат вписано прямокутник так, що на кожній стороні квадрата лежить по одній вершині прямокутника, а сторони прямокутника паралельні діагоналям квадрата. Знайдіть периметр прямокутника, якщо діагональ квадрата дорівнює d см.
Розв'язок:
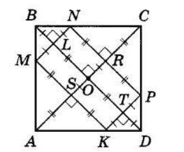
У квадраті ABCD AC ⊥ BD.
MN || AC за умовою, тоді MN ⊥ BD.
∠ABD = ∠CBD = $\frac{1}{2}$ ∠B =
= 90° : 2 = 45° (за властивістю діагоналей квадрата).
У △MBN BL — висота і бісектриса,
тоді △MBN — рівнобедрений, і L — середина MN.
У △BLN ∠NBL = ∠BNL = 45°, тоді BL = NL.
Аналогічно, розглянувши решту трикутників, отримаємо, що NR = RC = RP,
PT = DT = KT.
KS = AS = MS.
PMPNK = 2(MN + NP) =
= 2 · AC = 2d (см).
Відповідь:
2d см.
