Завдання № 40

ВПР 1 №40 Геометрія =  ВПТ 2 №40 Математика

На сторонах AB, BC, CD, DA квадрата ABCD позначено точки A₁, B₁, C₁, D₁ так, що AA₁ = BB₁ = CC₁ = DD₁. Визначте вид чотирикутника A₁B₁C₁D₁.

Розв'язок:

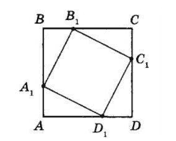
△A₁BB₁ = △B₁CC₁ =
= △C₁DD₁ = △D₁AA₁, за двома катетами
(AA₁ = BB₁ = CC₁ = DD₁, за умовою,
A₁B = B₁C = C₁D = D₁A, як частини рівних сторін квадрата без рівних відрізків).  
Тоді A₁B₁ = B₁C₁ = C₁D₁ = A₁D₁.
A₁B₁C₁D — ромб.  
∠B₁A₁D₁ =
= 180° − (∠D₁A₁A + ∠BA₁B₁);
∠A₁B₁C₁ =  
= 180° − (∠CB₁C₁ + ∠BB₁A₁);
∠B₁C₁D₁ =
= 180° − (∠B₁C₁C + ∠DC₁D₁);
∠C₁D₁A₁ =
= 180° − (∠C₁D₁D + ∠A₁D₁A).
З рівності трикутників 
∠BA₁B₁ = ∠CB₁C₁ =
= ∠DC₁D₁ = ∠A₁D₁A,
∠BB₁A₁ = ∠CC₁B₁ =
= ∠DD₁C₁ = ∠AA₁D₁.
Тоді ∠B₁A₁D₁ = ∠A₁B₁C₁ =
= ∠B₁C₁D₁ = ∠C₁D₁A₁.
Ромб A₁B₁C₁D₁, у якого всі кути рівні, є квадратом.

Відповідь:

квадрат.