Завдання № 9.29

№ 9.29 Геометрія =  № 17.29 Математика

У рівнобічній трапеції основи дорівнюють a і b (a > b), а гострий кут —   60°. Знайдіть:

1. бічну сторону трапеції;
2. периметр трапеції;
3. чи можна в трапецію вписати коло.

Розв'язок:

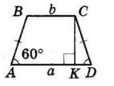
ABCD — трапеція, AB = CD, AD = a,
BC = b (a > b).  
∠BAD = ∠CDA = 60°. Проведемо BK ⊥ AD — висоту трапеції.  
У ΔCKD ∠DCK = 90° − ∠CDK =
= 90° − 60° = 30°,  
KD = $\frac{AD\ -\ BC}{2} = \frac{a\ -\ b}{2}. $ 
1. CD = 2KD = 2$\frac{a\ -\ b}{2}$ = a – b (за властивістю катета, що лежить проти кута 30°).  

2. P_ABCD = 2AB + BC + AD =
= 2(a – b) + b + a =
= 2a – 2b + b + a = 3a – b.

3. AB + CD = BC + AD;
2(a − b) = a + b;  
2a − a = 2b + b;  
a = 3b.  

Відповідь:

a = 3b.