№ 8.16 Геометрія = № 16.16 Математика
З точки кола проведено дві взаємно перпендикулярні хорди, які віддалені від центра на відстані 5 см і 7 см. Знайдіть довжини цих хорд.
Розв'язок:
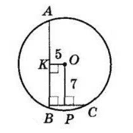
AB і BC — хорди, OK ⊥ AB, OK = 5 см — відстань від центру O кола до хорди AB; OP ⊥ BC = 7 см — відстань від центру O кола до хорди BC. Чотирикутник KOPB — прямокутник (три кути прямі);
OP = KB = 7 см, OK = PB = 5 см. За властивістю хорди, перпендикуляр до радіуса, K — середина AB, P — середина BC.
Отже, AB = 2KB = 2 ⋅ 7 = 14 (см),
BC = 2BP = 2 ⋅ 5 = 10 (см).
Відповідь:
14 см, 10 см.
