№ 7.14 Геометрія = № 15.14 Математика
AB — основа рівнобедреного трикутника ABC, O — центр описаного кола. ∠ AOB = a (a < 180°). Знайдіть кути трикутника ABC. Скільки випадків слід розглянути?
Розв'язок:
Можливі два випадки.
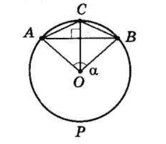
I випадок.
Центр описаного кола знаходиться поза трикутником.
∠AOB = ᴗACB = α, тоді вписаний
∠ACB = $\frac{1}{2}$ ᴗAPB = $\frac{1}{2}$ (360° − α) =
= 180° − $\frac{\alpha}{2}. $
∠CAB = ∠CBA = $\frac{180° − (180° − \frac{\alpha}{2})}{2}$ = $\frac{\alpha}{4}.$
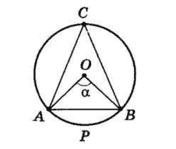
II випадок.
Центр описаного кола знаходиться всередині трикутника.
∠AOB = ᴗAPB = α.
∠ACB = $\frac{1}{2}$ ᴗAPB = $\frac{\alpha}{2}. $
∠CAB = ∠CBA = (180° − $\frac{\alpha}{2}$) = 90° − $\frac{\alpha}{4}. $
Відповідь:
1. $180° − \frac{\alpha}{2}; \frac{\alpha}{4};\ \frac{\alpha}{4}. $
2. $\frac{\alpha}{2}; 90° − \frac{\alpha}{4}; 90° − \frac{\alpha}{4}.$
