№ 6.38 Геометрія = № 14.38 Математика
Побудуйте трапецію за основами a і b (a > b) та бічними сторонами c і d.
Розв'язок:
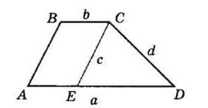
Нехай трапеція ABCD має основи
AD = a, BC = b
і бічні сторони AB = c, CD = d.
Проведемо відрізок CE || AB.
В ΔCDE CD = d, CE = c, DE = a − b.
Будуємо ΔCDE за трьома сторонами c, d, a − b.
Продовжуємо відрізок DE на AE = b, отримуємо вершину A трапеції.
Проводимо з точки C пряму, паралельну AD і відкладаємо CB = b.
ABCD — шуканa трапеція.
