№ 5.29 Геометрія = № 9.29 Математика
Бісектриса кута B у прямокутнику ABCD ділить сторону AD на відрізки AK і KD так, що AK : KD = 3 : 5. Знайдіть сторони прямокутника, якщо його периметр дорівнює 110 см.
Розв'язок:
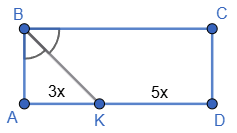
ABCD — прямокутник, бісектриса BK перетинає сторону AD у точці K.
AK : KD = 3 : 5.
Тоді AK = 3x, KD = 5x.
∠AKB = ∠KBC як внутрішні різносторонні при BC ∥ AD і січній BK. Тоді ∠BKA = ∠AKB, ∆ABK рівнобедрений, AB = AK = 3x.
CD = AB = 3x, AD = BC = 3x + 5x = 8x як протилежні сторони прямокутника.
PABCD = 2(AB + AD) = 2(3x + 8x) = 22x.
За умовою 22x = 110, x = 5.
Тоді AB = CD = 3 · 5 = 15 (см),
BC = AD = 5 · 8 = 40 (см).
Відповідь:
15 см; 40 см.
