№ 4.42 Геометрія = № 8.42 Математика
(Київська міська олімпіада, 1987 р.) Вписане в трикутник ABC коло дотикається до сторони BC у точці K . Доведіть, що відрізок AK довший за діаметр кола.
Розв'язок:
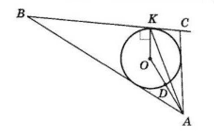
Розглянемо ∆AOK.
За нерівністю трикутника:
OK < AK − OA ; OK < AK − OD − DA ;
OK + OD < AK − DA ;
d < AK − DA .
Оскільки DA > O, то очевидно, що d < AK.
