№ 4.39 Геометрія = № 8.39 Математика
У чотирикутнику ABCD бісектриса кута A перетинає бісектриси кутів B і D під прямим кутом. Визначте вид чотирикутника ABCD.
Розв'язок:
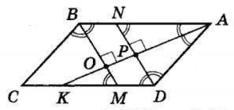
ABCD — чотирикутник. AK, BM і DN — бісектриси кутів A, B і D відповідно.
DN ⊥ AK, BM ⊥ AK за умовою.
Тоді BM || DN за ознакою (дві прямі, перпендикулярні третій, паралельні).
∆APN = ∆ADP за спільним катетом AP і гострим кутом (∠NAP = ∠DAP за умовою).
Звідси ∆ANP = ∆ADP.
∠ANP = ∠NDC — внутрішні різносторонні при прямих AB || CD і січній ND.
За ознакою AB || CD.
MBDN — паралелограм за означенням. ∠NBM = ∠NDM = ∠CBM, ∠NBM = ∠BMC як внутрішні різносторонні. Тоді ∆MCB = ∆NAD за стороною і прилеглими кутами. Звідси BC = AD, ∠A = ∠C, AB = CD.
ABCD — паралелограм.
