№ 4.23 Геометрія = № 8.23 Математика
Знайдіть кути ромба, якщо його сторона утворює з діагоналями кути, різниця яких дорівнює 10°.
Розв'язок:
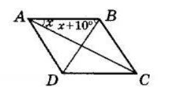
ABCD — ромб. Сторона AB утворює з діагоналями кути BAC і ABD.
Нехай ∠BAC = x, тоді ∠ABD = x + 10°.
∠A = 2x, ∠B = 2(x + 10°) за властивостями діагоналей ромба.
∠A + ∠B = 180° як сусідні.
2x + 2(x + 10) = 180;
4x + 20 = 180;
4x = 160;
x = 40.
Отже, ∠A = ∠C = 2 · 40° = 80°;
∠B = ∠D = 2 · (40° + 10°) = 100°.
Відповідь:
80°, 100°, 80°, 100°.
