№ 2.40 Геометрія = № 6.40 Математика
Зовнішній кут трикутника у 2 рази більший за один з внутрішніх кутів, не суміжний з ним. Доведіть, що трикутник є рівнобедреним.
Розв'язок:
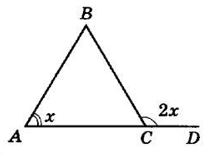
∠BCD — зовнішній кут трикутника ABC.
Нехай ∠A = x, тоді ∠BCD = 2x за умовою.
∠BCA = 180° − 2x (як суміжний з ∠BCD).
Сума кутів ΔABC дорівнює 180°:
∠B = 180° − (∠A + ∠BCA);
∠B = 180° − (x + (180° − 2x));
∠B = 180° − x − 180° + 2x = x.
Отже, ∠B = ∠A, значить, ΔABC — рівнобедрений.
