№ 2.33 Геометрія = № 6.33 Математика
Бісектриса кута B паралелограма ABCD ділить сторону AD на два відрізки AK і KD так, що AK − KD = 1 см. Знайдіть сторони паралелограма, якщо його периметр дорівнює 40 см.
Розв'язок:
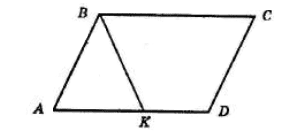
За умовою задачі ∠ABK = ∠CBK і AK − KD = 4 см.
Але ∠CBK = ∠AKB як внутрішні різносторонні при паралельних прямих BC і AD і січній BK.
Тому ΔABK — рівнобедрений, AB = AK = x см.
Тоді KD = (x – 1) см, AD = (2x − 1) см.
Периметр паралелограма дорівнює (x + 2x – 1) · 2,
що за умовою становить 40 см.
(AB + BC) = 40 см.
(x + 2x – 1) · 2 = 40;
3x – 1 = 20;
3x = 21;
x = 7.
Отже, AB = AK = 7 см, AD = 7 + 7 – 1 = 13 (см). BC = AD = 13 см; CD = AB = 7 см.
Відповідь:
7 см, 13 см.
