№ 2.17 Геометрія = № 6.17 Математика
У чотирикутнику ABCD ∠ 1 = ∠ 2, ∠ 3 = ∠ 4. Доведіть, що ABCD — паралелограм.
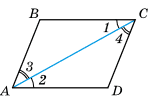
Розв'язок:
1. ∠BAD = ∠2 + ∠3; ∠BCD = ∠1 + ∠4.
Але ∠1 = ∠2; ∠3 = ∠4, тому ∠BAD = ∠BCD.
2. ∠B = 180° − (∠1 + ∠3); ∠D = 180° − (∠2 + ∠4).
Оскільки ∠2 = ∠1, ∠3 = ∠4, то ∠B = ∠D.
3. Оскільки у чотирикутнику ABCD протилежні кути попарно рівні, то він є паралелограмом, що й треба було довести.
