№ 2.10 Геометрія = № 6.10 Математика
Знайдіть усі кути паралелограма, якщо:
1. сума двох з них дорівнює 200°;
2. один з них на 40° менший від другого;
3. один з них удвічі більший за другий;
4. градусні міри двох з них відноситься як 4 : 5.
Розв'язок:
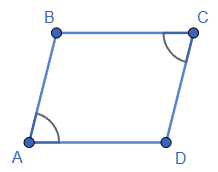
1. ∠B + ∠D = 200°; ∠B = ∠D = $\frac{200°}{2}$ = 100°.
Тоді ∠A = ∠C = 180° − 100° = 80°.
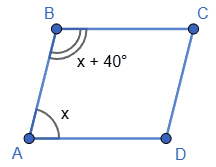
2. Нехай ∠A = x, тоді ∠B = x + 40°.
Маємо x + x + 40 = 180;
2x = 140;
x = 70.
Отже, ∠A = ∠C = 70°;
∠B = ∠D = 70° + 40° = 110°.
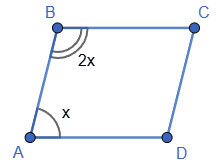
3. Нехай ∠A = x, тоді ∠B = 2x.
Маємо x + 2x = 180;
3x = 180;
x = 60.
Отже, ∠A = ∠C = 60°;
∠B = ∠D = 60° · 2 = 120°.
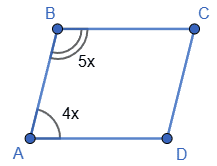
4. Оскільки ∠A : ∠B = 4 : 5,
то можна позначити
∠A = 4x, ∠B = 5x.
Маємо 4x + 5x = 180;
9x = 180;
x = 20.
Отже, ∠A = ∠C = 4 · 20° = 80°;
∠B = ∠D = 5 · 20° = 100°.
