№ 1.34 Геометрія = № 5.34 Математика
(Всеукраїнська олімпіада з математики, 1964 р.)
Знайдіть найбільше значення n, для якого n точок можна розмістити на площині так, щоб кожні три з них були вершинами прямокутного трикутника.
Розв'язок:
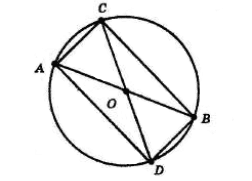
Нехай A і B — ті з даних точок, відстань між якими найбільша, а C — будь−яка з інших даних точок.
У ΔABC за умовою один з кутів прямий. Оскільки AB — найбільша сторона трикутника, то ∠ACB = 90°.
Отже, усі дані точки лежать на колі, побудованому на відрізку AB як на діаметрі.
Припустимо, що серед даних точок, крім точки C, є й точка D. У ΔADC — один з кутів прямий.
∠ADC не може бути прямим, бо тоді точка C збігалася б з точкою B (відрізок AC був би діаметром кола).
Аналогічно ∠ACD також не може бути прямим. Тому ∠DAC = 90°, а отже, DC — діаметр кола.
Довели, що будь−яка інша четверта точка D є кінцем діаметра кола, який проходить через точку C.
Така точка єдина. Отже, n = 4.
Відповідь:
n = 4.
