№ 1.29 Геометрія = № 5.29 Математика
У прямокутному трикутнику гострий кут дорівнює 60°, а сума меншого катета й медіани, проведеної до гіпотенузи, — 10 см. Знайдіть гіпотенузу цього трикутника.
Розв'язок:
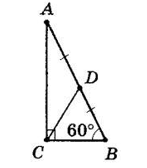
У ΔABC ∠C = 90°, ∠B = 60°, CD — медіана.
За властивістю медіани прямокутного трикутника, що проведена до гіпотенуза, маємо:
CD = АВ : 2 = AD = BD.
∠A = 90° − ∠B = 30°. Тоді BC — менший катет, оскільки лежить проти меншого кута. За умовою CD + BC = 10 см.
У ΔBCD CD = BD, ∠B = 60°,
тоді ΔBCD — рівносторонній,
CD = BC = 10 см : 2 = 5 см.
AB = 2CD = 2 · 5 см = 10 см.
Відповідь:
10 см.
