№ 10.9 Геометрія = № 18.9 Математика
K – точка перетину діагоналей BD трапеції ABCD з її середньою лінією MN. Доведіть, що BK = KD.
Розв'язок:
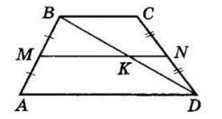
Діагональ BD перетинає середню лінію MN у точці K. За властивістю середньої лінії MN || AD, M — середина AB, тоді за теоремою Фалеса K — середина BD.
Отже, BK = KD.
