№ 10.28 Геометрія = № 18.28 Математика
У прямокутній трапеції тупий кут дорівнює 120°, більша основа – 14 см, а більша бічна сторона – 8 см. Знайдіть меншу основу трапеції.
Розв'язок:
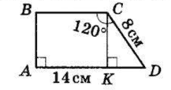
В трапеції ABCD ∠A = ∠B = 90°,
∠C = 120°.
AD = 14 см, CD = 8 см (найбільша бічна сторона, бо похила більша за перпендикуляр).
Проводимо CK ⊥ AD. ΔBCK — прямокутник (BC || AK, AB || CK, ∠A = 90°).
∠DCK = ∠BCD − ∠BCK =
= 120° − 90° = 30°.
Тоді у ΔCKD KD = $\frac{1}{2}$ CD =
= $\frac{1}{2}$ · 8 = 4 (см) (за властивістю катета, що лежить проти кута 30°).
У прямокутнику ABCD
AK = BC = AD − KD =
= 14 − 4 = 10 (см).
Відповідь:
10 см.
