№ 67 Геометрія = № 67 Математика
Рівнобедрений трикутник ABC з основою AB вписано у коло із центром у точці O, ∠AOB = 100°. Знайдіть кути трикутника ABC. Скільки розв’язків має задача?
Розв'язок:
Ⅰ розв’язок
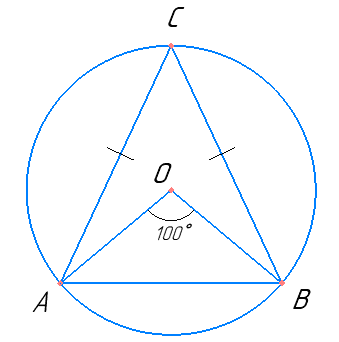
∠AOB – центральний кут;
∠ACB – вписаний кут;
Вписаний кут у колі дорівнює половині відповідного центрального кута (це випливає із теореми про вписаний кут), тоді:
∠ACB = ∠AOB : 2 = 100° : 2 = 50°;
Кути при основі рівнобедреного трикутника рівні:
∠CBA = ∠CAB = x;
Сума кутів трикутника рівна 180°:
∠ACB + ∠CBA + ∠CAB = 180°,
50° + х + х = 180°,
2х = 130°,
х = 65°.
Ⅱ розв’язок
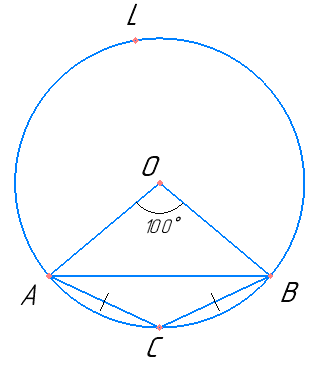
∠AOB – центральний кут;
∠ACB – вписаний кут;
◡ACB = ∠AOB = 100°,
◡ALB = 360° − ◡ACB = 360° − 100° = 260°;
Вписаний кут вимірюється половиною дуги на яку він опирається (згідно теореми про вписаний кут):
∠ACB = ◡ALB : 2 = 260° : 2 = 130°;
Кути при основі рівнобедреного трикутника рівні:
∠CBA = ∠CAB = (180° − ∠ACB) : 2 =
= (180° − 130°) : 2 = 50° : 2 = 25°.
Відповідь:
Ⅰ. 65°, 65°, 50°.
Ⅱ. 25°, 25°, 130°.
