№ 5 ЗПС Алгебра = № 5 ЗПС Математика
Доведіть одну з тотожностей видатного математика Л. Ейлера (1707–1783):
$\left(\frac{a\left(a^3+2b^3\right)}{a^3-b^3}\right)^3-\left(\frac{b\left(2a^3+b^3\right)}{a^3-b^3}\right)^3=$
$= a^3+b^3.$
Розв'язок:
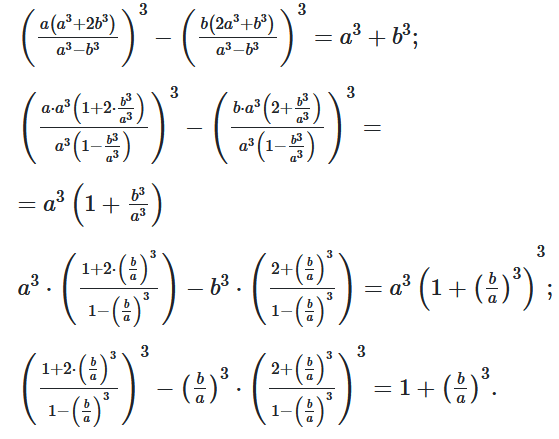
Нехай $\left(\frac{b}{a}\right)^3=t,$ тоді
$\left(\frac{1+2t}{1-t}\right)^3-t\cdot\left(\frac{2+t}{1-t}\right)^3=1+t;$
$\frac{(1+2t)^3-t(2+t)^3}{(1-t)^3}=$
$= \frac{1+6t+12t^2+8t^3-8t-12t^2-6t^3-t^4}{(1-t)^3}=$
$= \frac{2t^3-2t-t^4+1}{(1-t)^3}=$
$= \frac{\left(2t^3-2t\right)-\left(t^4-1\right)}{(1-t)^3}=$
$= \frac{2t\left(t^2-1\right)-\left(t^2-1\right)\left(t^2+1\right)}{(1-t)^3}=$
$= \frac{\left(t^2-1\right)\left(2t-t^2-1\right)}{(1-t)^3}=$
$= -\frac{\left(t^2-1\right)\left(t^2-2t+1\right)}{(1-t)^3}=$
$= \frac{\left(t^2-1\right)(t-1)^2}{(t-1)^3}=$
$= \frac{(t-1)(t+1)(t-1)^2}{(t-1)^3}=$
$= \frac{(t-1)^3(t+1)}{(t-1)^3}=t+1.$
$t+1=t+1,$ що й треба було довести.
