№ 3 ЗПС Алгебра = № 3 ЗПС Математика
Спростіть вираз:
1. $\frac{\frac{1}{x}-\frac{1}{y+z}}{\frac{1}{x}+\frac{1}{y+z}}\cdot\left(1+\frac{y^2+z^2-x^2}{2yz}\right):$
$ : \frac{x-y-z}{xyz};$
2. $\frac{\frac{m-n}{2m-n}-\frac{m^2+n^2+m}{2m^2+mn-n^2}}{\left(4n^4+4mn^2+m^2\right):\left(2n^2+m\right)}\cdot$
$\cdot\left(n^2+n+mn+m\right);$
3. $\frac{4}{x+\frac{1}{y+\frac{1}{z}}}:\frac{1}{x+\frac{1}{y}}-\frac{4}{y(xyz+x+z)};$
4. $\left(\left(\frac{a}{b-a}\right)^{-2}-\frac{(a+b)^2-4ab}{a^2-ab}\right)^2\cdot$
$\cdot\frac{a^4}{a^2b^2-b^4};$
5. $\frac{p^{-6}-64}{4+2p^{-1}+p^{-2}}\cdot\frac{p^2}{4-4p^{-1}+p^{-2}}-$
$-\frac{4p^2(2p+1)}{1-2p};$
6. $\frac{x^{-1}-y^{-1}}{x^{-3}+y^{-3}}:\frac{x^2y^2}{(x+y)^2-3xy}\cdot$
$\cdot\left(\frac{x^2-y^2}{xy}\right)^{-1}.$
Розв'язок:
1. $\frac{\frac{1}{x}-\frac{1}{y+z}}{\frac{1}{x}+\frac{1}{y+z}}\cdot\left(1+\frac{y^2+z^2-x^2}{2yz}\right):$
$ : \frac{x-y-z}{xyz};$
а) $1+\frac{y^2+z^2-x^2}{2yz}=\frac{2yz+y^2+z^2-x^2}{2yz}=$
$= \frac{(y+z)^2-x^2}{2yz}=\frac{(y+z-x)(y+z+x)}{2yz};$
б) $\frac{1}{x}-\frac{1}{y+z}=\frac{y+z-x}{x(y+z)};$
в) $\frac{1}{x}+\frac{1}{y+z}=\frac{y+z+x}{x(y+z)};$
г) $\frac{y+z-x}{x(y+z)}:\frac{y+x+z}{x(y+z)}=$
$= \frac{(y+z-x)\cdot x(y+z)}{x(y+z)(y+z+x)}=\frac{y+z-x}{y+z+x};$
д) $\frac{y+z-x}{y+z+x}\cdot\frac{(y+z-x)(y+z+x)}{2yz}=$
$= \frac{(y+z-x)^2}{2yz};$
е) $\frac{(y+z-x)^2}{2yz}:\frac{x-y-z}{xyz}=$
$= \frac{(y+z-x)^2\cdot x y z}{2yz\cdot(x-y-z)}=\frac{x\cdot(x-(y+z))^2}{2(x-y-z)}=$
$= \frac{x\cdot(x-y-z)^2}{2(x-y-z)}=\frac{(x-y-z)x}{2};$
2. $\frac{\frac{m-n}{2m-n}-\frac{m^2+n^2+m}{2m^2+mn-n^2}}{\left(4n^4+4mn^2+m^2\right):\left(2n^2+m\right)}\cdot$
$\cdot\left(n^2+n+mn+m\right);$
а) $ \frac{m-n}{(2m-n)}-\frac{m^2+n^2+m}{m^2+m^2+mn-n^2}=$
$= \frac{m-n}{2m-n}-\frac{m^2+n^2+m}{\left(4m^2-n^2\right)-\left(2m^2-mn\right)}=$
$= \frac{m-n}{2m-n}-$
$- \frac{m^2+n^2+m}{(2m-n)(2m+n)-m(2m-n)}=$
$= \frac{m-n}{2m-n}-\frac{m^2+n^2+m}{(2m-n)(2m+n-m)}=$
$= \frac{(m-n)(m+n)-\left(m^2+n^2+m\right)}{(2m-n)(m+n)}=$
$= \frac{m^2-n^2-m^2-n^2-m}{(2m-n)(m+n)}=$
$= -\frac{2n^2+m}{(2m-n)(m+n)};$
б) $\frac{4n^4+4mn^2+m^2}{2n^2+m}=\frac{\left(2n^2+m\right)^2}{2n^2+m}=$
$= 2n^2+m;$
в) $-\frac{2n^2+m}{(2m-n)(m+n)}:\frac{2n^2+m}{1}=$
$= -\frac{2n^2+m}{(2m-n)(m+n)\left(2n^2+m\right)}=$
$= \frac{1}{(n-2m)(m+n)};$
г) $\frac{1}{(n-2m)(m+n)}\cdot$
$\cdot\left(n^2+n+mn+m\right)=$
$= \frac{n(n+1)+m(n+1)}{(n-2m)(m+n)}=$
$= \frac{(n+1)(m+n)}{(n-2m)(m+n)}=\frac{n+1}{m-2m}.$
3. $\frac{4}{x+\frac{1}{y+\frac{1}{z}}}:\frac{1}{x+\frac{1}{y}}-\frac{4}{y(xyz+x+z)}=4;$
a) $\frac{1}{y+\frac{1}{z}}=\frac{z}{yz+1};$
б) $x+\frac{z}{yz+1}=\frac{xyz+x+z}{yz+1};$
в) $\frac{\frac{4}{xyz+x+z}}{yz+1}= \frac{4(yz+1)}{xyz+x+z};$
г) $\frac{4(yz+1)}{xyz+x+z}:\frac{1}{x+\frac{1}{y}}=$
$= \frac{4(yz+1)}{xyz+x+z}:\frac{y}{xy+1}=$
$= \frac{4(yz+1)(xy+1)}{y(xyz+x+z)};$
д) $\frac{4(yz+1)(xy+1)}{y(xyz+x+z)}-\frac{4}{y(xyz+x+z)}=$
$= \frac{4\left(y^2xz+yz+xy+1-1\right)}{y(xyz+x+z)}=$
$= \frac{4y(xyz+z+x)}{y(xyz+x+z)}=4;$
4. $\left(\left(\frac{a}{b-a}\right)^{-2}-\frac{(a+b)^2-4ab}{a^2-ab}\right)^2\cdot$
$\cdot\frac{a^4}{a^2b^2-b^4};$
а) $\left(\frac{a}{b-a}\right)^{-2}=\left(\frac{b-a}{a}\right)^2=$
$= \frac{(b-a)^2}{a^2}=\frac{(a-b)^2}{a^2};$
б) $\frac{(a-b)^2}{a^2}-\frac{(a+b)^2-4ab}{a(a-b)}=$
$= \frac{(a-b)^3-a\left(a^2+2ab+b^2-4ab\right)}{a^2(a-b)}=$
$= \frac{a^3-3a^2b+3ab^2-b^3-a^3+2a^2b-ab^2}{a^2(a-b)}=$
$= \frac{-b^3-a^2b+2ab^2}{a^2(a-b)}=$
$= \frac{-b\left(b^2+a^2-2ab\right)}{a^2(a-b)}=$
$= \frac{-b(a-b)^2}{a^2(a-b)}=\frac{-b(a-b)}{a^2}=$
$= \frac{b(b-a)}{a^2};$
в) $\frac{b^2(b-a)^2}{a^4}\cdot\frac{a^4}{a^2b^2-b^4}=\frac{b^2(a-b)^2}{b^2\left(a^2-b^2\right)}=$
$= \frac{(a-b)^2}{(a-b)(a+b)}=\frac{a-b}{a+b};$
5. $\frac{p^{-6}-64}{4+2p^{-1}+p^{-2}}\cdot\frac{p^2}{4-4p^{-1}+p^{-2}}-$
$-\frac{4p^2(2p+1)}{1-2p};$
a) $\ p^{-6}-64=\frac{1}{p^6}-64=$
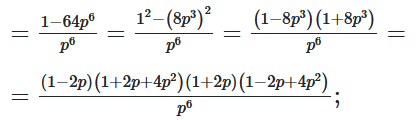
б) $4+2p-1+p-2=$
$= 4+2p\ 4+2p^{-1}+p^{-2}=$
$= 4+\frac{2}{p}+\frac{1}{p^2}=\frac{4p^2+2p+1}{p^2};$
в) $ 4-4p^{-1}+p^{-2}=$
$= 4-\frac{4}{p}+\frac{1}{p^2}=\frac{4p^2-4p+1}{p^2}=$
$= \frac{(2p-1)^2}{p^2};$
г) $\frac{(1-2p)\left(1+2p+4p^2\right)(1+2p)\left(1-2p+4p^2\right)}{p^6}\cdot$
$\cdot\frac{p^2}{4p^2+2p+1}\cdot\frac{p^4}{(1-2p)^2}=$
$= \frac{(1+2p)\left(1-2p+4p^2\right)}{1-2p};$
д) $\frac{1+8p^3}{1-2p}-\frac{4p^2(2p+1)}{1-2p}=$
$= \frac{1+8p^3-8p^3-4p^2}{1-2p}=$
$= \frac{1-4p^2}{1-2p}=\frac{(1-2p)(1+2p)}{1-2p}=$
$= 1+2p;$
6. $\frac{x^{-1}-y^{-1}}{x^{-3}+y^{-3}}:\frac{x^2y^2}{(x+y)^2-3xy}\cdot$
$\cdot\left(\frac{x^2-y^2}{xy}\right)^{-1}.$
а) $\frac{x^{-1}-y^{-1}}{x^{-3}+y^{-3}}=\frac{\frac{1}{x}-\frac{1}{y}}{\frac{1}{x^3}+\frac{1}{y^3}}=\frac{\frac{y-x}{xy}}{\frac{x^3+y^3}{x^3y^3}}=$
$= \frac{(y-x)\cdot x^3y^3}{xy\cdot\left(x^3+y^3\right)}=\frac{x^2y^2(y-x)}{x^3+y^3};$
б) $\frac{x^2y^2(y-x)}{x^3+y^3}:\frac{x^2y^2}{(x+y)^2-3xy}=$
$= \frac{x^2y^2(y-x)\cdot\left(x^2-xy+y^2\right)}{(x+y)\left(x^2-xy+y^2\right)\cdot x^2y^2}=\frac{y-x}{x+y};$
в) $\frac{y-x}{x+y}\cdot\frac{xy}{x^2-y^2}=$
$= -\frac{xy\cdot(x-y)}{(x+y)(x-y)(x+y)}=-\frac{xy}{(x+y)^2}.$
