№ 15 ЗПС Алгебра = № 15 ЗПС Математика
Знайдіть значення виразу:
1. $\sqrt{3-\sqrt{13-4\sqrt3}};$
2. $\sqrt{\sqrt6-\sqrt{6-\sqrt{25-4\sqrt6}}};$
3. $\sqrt{|30\sqrt3-52|}-$
$- \sqrt{52+30\sqrt3}.$
Розв'язок:
1. $\sqrt{3-\sqrt{13-4\sqrt3}}=$
$= \sqrt{3-\sqrt{(2\sqrt3-1)^2}}=$
$= \sqrt{3-|2\sqrt3-1|}=$
$= \sqrt{3-(2\sqrt3-1)}=$
$= \sqrt{3-2\sqrt3+1}=$
$= \sqrt{4-2\sqrt3}=$
$= \sqrt{(1-\sqrt3)^2}= |1-\sqrt3|=$
$= -(1-\sqrt3)= \sqrt3-1;$
2. $ \sqrt{\sqrt6-\sqrt{6-\sqrt{25-4\sqrt6}}}=$
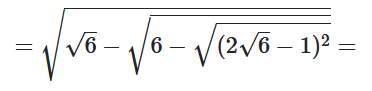
$= \sqrt{\sqrt6-\sqrt{6-|2\sqrt6-1|}}=$
$= \sqrt{\sqrt6-\sqrt{6-(2\sqrt6-1)}}=$
$= \sqrt{\sqrt6-\sqrt{6-2\sqrt6+1}}=$
$= \sqrt{\sqrt6-\sqrt{7-2\sqrt6}}=$
$= \sqrt{\sqrt6-\sqrt{(1-\sqrt6)^2}}=$
$= \sqrt{\sqrt6-|1-\sqrt6|}=$
$= \sqrt{\sqrt6+(1-\sqrt6)}=$
$= \sqrt{\sqrt6+1-\sqrt6}=$
$= \sqrt1=1;$
3. $\sqrt{|30\sqrt3-52|}-$
$- \sqrt{52+30\sqrt3}=A;$
$A^2=|30\sqrt3-52|+$
$+ (52+30\sqrt3)-$
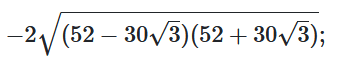
$A^2=52-30\sqrt3+52+$
$+ 30\sqrt3-2\sqrt{2704-2700};$
$ A^2=104-2\sqrt4;$
$A^2=104-4;A^2=100;$
$A=\pm10.$
Оскільки $52-30\sqrt3<52+30\sqrt3,$ то $A<0.$
Відповідь:
$–10.$
