№ 16.32 Алгебра = № 32.32 Математика
(Київська математична олімпіада, 1989 р.) Двоє гравців по черзі здійснюють хід за такими правилами: у клітинках нескінченного аркуша один гравець ставить хрестики, а другий – нулики. Чи може другий гравець грати так, щоб перший ніколи не зміг заповнити хрестиками якийсь квадрат 2 · 2?
Розв'язок:
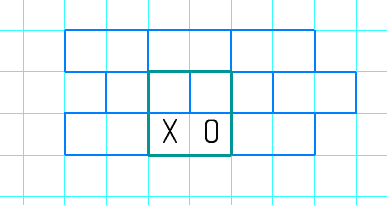
Уявімо, що всі клітинки сітки заздалегідь розбито на «кістки доміно» розміру 1 × 2 (тобто на прямокутники, що покривають по дві сусідні клітинки). Нехай це розбиття зафіксоване й більше не змінюється.
Другий гравець може дотримуватися такої стратегії:
якщо перший гравець у деякій клітинці однієї з кісток доміно ставить хрестик, то другий гравець у відповідь ставить нулик у другій клітинці цієї ж кістки. Таким чином у кожній кістці доміно буде або один хрестик і один нулик, або взагалі нічого, але ніколи — два хрестики.
Зауважимо, що будь-який квадрат 2 × 2 обов’язково містить принаймні одну цілу кістку доміно (тобто обидві клітинки якої входять до цього квадрата). А отже, у кожному квадраті 2 × 2 є хоча б одна клітинка з нуликом (бо в цій кістці не можуть стояти два хрестики).
Отже, перший гравець ніколи не зможе заповнити всі чотири клітинки якогось квадрата 2 × 2 хрестиками. Тому другий гравець справді може грати так, щоб квадрат 2 × 2 з одних лише хрестиків ніколи не з’явився.
Відповідь:
Так.
