: Варіант 2 ДР-1 [2М]

Завдання № 9 ДР-1 [2М] Варіант 2

Діагностична робота (сторінка 13)

Тема: Чотирикутник, його елементи. Паралелограм та його види

Бісектриса кута B паралелограма ABCD ділить сторону AD на два відрізки AK і KD так, що AK : KD = 4 : 3. Знайдіть сторони паралелограма, якщо його периметр дорівнює 66 см.

Розв’язок:

Відповідь до завдання № 9 ДР 1 вар 2 Геометрія

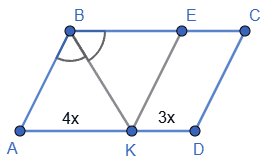
1. Нехай AK = 4x, KD = 3x (за умовою AK : KD = 4 : 3).

2. Проведемо через точку K пряму KE ∥ AB до перетину з BC в точці E. Тоді ABEK — паралелограм (бо AB ∥ KE, AK ∥ BE). Оскільки BK — бісектриса ∠B і водночас діагональ паралелограма ABEK, то ABEK є ромбом (ознака: якщо діагональ паралелограма ділить кут навпіл, то паралелограм — ромб). Отже, AB = AK.

3. Маємо AB = AK = 4x. Крім того, AD = BC (властивість паралелограма) і AD = AK + KD = 4x + 3x = 7x, отже BC = 7x.

4. Периметр:
P = 2(AB + BC) = 66
2(4x + 7x) = 66
22x = 66
x = 3.

5. Сторони:
AB = CD = 4x = 12 см;
BC = AD = 7x = 21 см.

Відповідь:

AB = CD = 12 см; BC = AD = 21 см.