Завдання № 25.34

№ 25.34 Геометрія =  № 48.34 Математика

Один з кутів ромба на 120° більший за другий, а сторона ромба дорівнює 6 см. Знайдіть площу ромба.

Розв'язок:

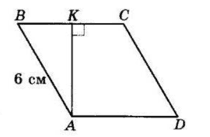
ABCD — ромб,

AB = BC = CD = AD = 6 см.

∠A = ∠B + 120°. Нехай ∠B = x, тоді

∠A = x + 120°.

x + x + 120° = 180; 

2x = 60;

x = 30°. Отже, ∠B = 30°.

Тоді висота AK = $\frac{1}{2}$ AB = 3 см (як катет, що лежить проти кута 30°).

S_ABCD = BC · AK =

= 6 · 3 = 18 (см²).

Відповідь:

18 см².