№ 24.34 Геометрія = № 47.34 Математика
Стіна заввишки 3,5 м відкидає тінь завдовжки 5 м. Олександр Семенович, зріст якого 1 м 75 см, стоїть на відстані 10 м від краю тіні. Яку найменшу кількість кроків він має зробити, щоб повністю потрапити в тінь, якщо довжина його кроку 0,5 м?
Розв'язок:
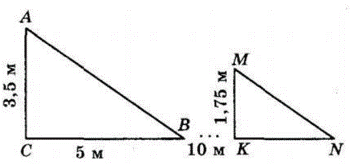
Об'єкт і його тінь — це катети двох подібних трикутників.
Знайдемо довжину тіні чоловіка.
$\frac{AC}{CB}=\ \frac{MK}{KN};$
$\frac{3,5}{5}\ =\ \frac{1,75}{KN};$
$KN\ = \frac{5 · 1,75}{3,5} = 2{,}5$ (м).
Щоб повністю потрапити в тінь, Олександр Семенович повинен переміститися в бік стіни на $10$ м +$ 2{,}5$ м = $12{,}5$ м.
Кількість кроків:
$12{,}5$ м : $0{,}5 = 25.$
Відповідь:
$25$ кроків.
