Завдання № 24.31

№ 24.31 Геометрія =  № 47.31 Математика

Бісектриса кута прямокутника ділить його діагональ у відношенні 1 : 2. Знайдіть площу прямокутника, якщо його периметр дорівнює 48 см. 

Розв'язок:

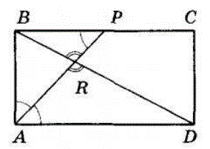
ABCD — прямокутник, AP — бісектриса кута A, BD — діагональ, K — точка їх перетину.

BK : KD = 1 : 2.

∠BPA = ∠PAD як внутрішні різносторонні при паралельних прямих AD і BC і січній AP.

Тоді в ΔABP ∠BAP = ∠BPA,

AB = BP.

ΔBKP ∼ ΔDKA за двома кутами (∠BPK = ∠KAD, ∠BKP = ∠AKD як вертикальні).

BK : KD = 1 : 2 за умовою,

тоді BP : AD = 1 : 2.

Нехай AB = x см,

тоді AD = 2x см.

P_ABCD = 2(AB + AD) =

= 2(x + 2x) = 6x.

За умовою 6x = 48 см,

звідки x = 8 см.

Отже, AB = 8 см,

AD = 2 · 8 = 16 см.

S_ABCD = AB · AD = 8 · 16 = 128 (см²).

Відповідь:

128 см².