№ 19.46 Геометрія = № 38.46 Математика
(Задача Архімеда). Якщо в колі хорди AB і CD перетинаються в точці E під прямим кутом, то сума квадратів відрізків AE, BE, CE і DE дорівнює квадрату діаметра. Доведіть це.
Розв'язок:
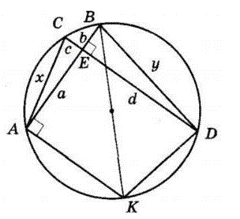
Нехай $a, b, c, d$ — дані відрізки хорд $AB$ і $CD.$
Нехай $AC = x, BD = y.$
Тоді за теоремою Піфагора для $ΔAED:$
$x^2 = a^2 + c^2.$ (1)
Для $ΔBEC: y^2 = b^2 + d^2. (2)$
Проведемо $AK || CD.$
Тоді $BK = 2R$ — діаметр (оскільки $AK || CD,$ а $AB ⊥ CD,$
то $AB ⊥ AK$).
$ACKD$ — рівнобічна трапеція, оскільки в коло можна вписати лише рівнобічну трапецію і $AK = KD = x.$
$∠BDK = 90° $ (спирається на діаметр).
За теоремою Піфагора для $ΔBDK:$
$BD^2 + KD^2 = BK^2;$
$x^2 + y^2 = (2R)^2;$
$a^2 + c^2 + b^2 + d^2 =$
$= 4R^2,$
тобто $AE^2 + BE^2 + CE^2 + DE^2 =$
$= 4R^2.$
