№ 18.29 Геометрія = № 37.29 Математика
(Задача Стенфордського університету.) Точку P так розташовано
всередині прямокутника так, що відстань від неї до вершини прямокутника дорівнює 5 ярдів, до протилежної вершини – 14 ярдів, до третьої вершини – 10 ярдів. Якою є відстань від точки P до четвертої вершини?
Розв'язок:
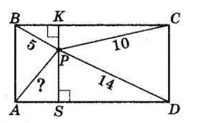
$ABCD$ — прямокутник.
$PB = 5, PC = 10, PD = 14.$
Проведемо $PK ⊥ BC$ і $PS ⊥ AD.$ Через точку $P$ можна провести тільки один спільний перпендикуляр до паралельних прямих $BC$ і $AD.$ Тоді $ABKS$ — прямокутник.
Нехай $AD = BC = b,$
$ BK = AS = x,$
тоді $KC = SD = b − x.$
З $∆BKP\ KP^2 = $
$= BP^2 − BK^2 =$
$= 5^2 − x^2 = 25 − x^2.$
З $∆PKC\ KP^2 =$
$= PC^2 − KC^2 =$
$= 10^2 − (b − x)^2 = $
$= 100 − b^2 + 2bx − x^2 =$
$= −b^2 + 2bx − x^2.$
Ліві частини рівностей однакові, значить, і праві частини рівні:
$25 − x^2 =$
$= 100 − b^2 + 2bx − x^2;$
$b^2 − 2bx – 75 = 0. (1) $
З $∆APS\ PS^2 =$
$= AP^2 – AS^2 = AP^2 − x^2.$
З $∆PSD\ PS^2 = PD^2 – SD^2 =$
$= 14^2 − (b − x)^2 =$
$= 196 − b^2 + 2bx − x^2;$
$AP^2 − x^2 =$
$= 196 − b^2 + 2bx − x^2;$
$AP^2 + b^2 − 2bx – 196 = 0. (2)$
3 $(1)$ і $(2): b^2 − 2bx − 75 =$
$= AP^2 + b^2 − 2bx − 196.$
$AP^2 = 196 − 75;$
$AP^2 = 121;$
$AP = 11.$
Відповідь:
$11$ ярдів.
