Завдання № 14.27

№ 14.27 Геометрія =  № 26.27 Математика

(Олімпіада Нью-Йорка, 1976 р.)  Висоти гострокутного трикутника ABC перетинаються в точці O, а на відрізках OB і OC позначено точки B₁ і C₁, для яких ∠AB1C = ∠AC1B = 90°. Доведіть, що AB1 = AC1.         

Розв'язок:

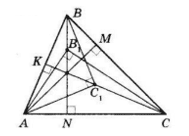
У ΔAB₁C, AB₁² = AN ⋅ AC.
У ΔAC₁B, C₁A² = AK ⋅ AB.
ΔABN ~ ΔACK за двома кутами (∠A — спільний, ∠CKA = ∠BNA = 90°).
Тоді:  $\frac{AC}{AB} = \frac{AK}{AN},$
звідки AC ⋅ AN = AB ⋅ AK.
Отже, AB₁² = AC₁²,
а оскільки AB₁ > 0 і AC₁ > 0, то AB₁ = AC₁.