№ 12.18 Геометрія = № 24.18 Математика
Точки K і L належать відповідно сторонам AB і AC трикутника ABC. Чи може точка перетину відрізків BL і KC ділити кожний з них навпіл?
Розв'язок:
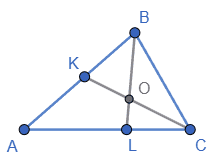
Припустимо, що точка O – перетин відрізків BL і KC – ділить кожний з них навпіл.
Тоді KO = OC, BO = OL,
∠KOB = ∠COL як вертикальні.
ΔKOB = ΔCOL за двома сторонами і кутом між ними.
З рівності трикутників випливає рівність відповідних кутів:
∠BKO = ∠LCO, але ці кути є внутрішніми різносторонніми при прямих AB і AC та січній KC.
Тоді AB || AC, що суперечить умові.
Отже, наше припущення хибне. Точка перетину відрізків не може ділити кожний із них навпіл.
Відповідь:
ні.
