ВПР 1 №35 Геометрія = ВПТ 2 №35 Математика
На сторонах прямокутника зовні нього побудовано рівносторонні трикутники. Доведіть, що вершини трикутників є вершинами ромба.
Розв'язок:
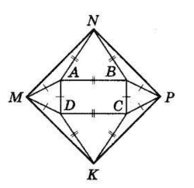
△MAN = △PBN = △MDK = △PSK за двома сторонами і кутом між ними
(AM = BP = CP = DM = AD = BC,
AN = BN = CK = DK = AB = CD;
∠MAN = ∠NBP = ∠PCK =
= ∠MDK = 360° − (60° + 90° + 60°) =
= 150°.
З рівності трикутників випливає, що
MN = PN = KP = KM.
Отже, MNPK — ромб.
