ВПР 1 №33 Геометрія = ВПТ 2 №33 Математика
Висота ромба дорівнює 10 см, а його периметр − 80 см. Знайдіть:
1. кути ромба;
2. кут між висотою, проведеною з вершини тупого кута ромба, і його меншою діагоналлю.
Розв'язок:
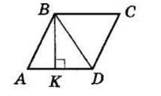
1. ABCD — ромб, BK ⊥ AD,
BK = 10 см — висота.
PABCD = 80 см,
тоді AB = BC = CD = AD =
= 80 : 4 = 20 (см).
Оскільки катет BK вдвічі менший від гіпотенузи AB, то він лежить напроти кута 30°.
Отже, ∠A = 30°, ∠C = ∠A = 30°.
∠B = ∠D = 180° − 30° = 150°.
2. ∠BDK = $\frac{1}{2}$ см ∠D =
= $\frac{1}{2}$ см · 150° = 75°.
∠KBD = 180° − (∠BKD + ∠BDK) =
= 180° − (90° + 75°) = 15°.
Відповідь:
1. 30°, 150°;
2. 15°.
