Завдання № 8.18

№ 8.18 Геометрія =  № 16.18 Математика

(Всеукраїнська олімпіада з математики, 1976 р.) У середині гострокутного трикутника ABC дано точку P таку, що  
∠ APB = ∠ ACB + 60°,   
∠ BPC = ∠ BAC + 60°,  
∠ CPA = ∠ CBA + 60°.  
Доведіть, що основи перпендикулярів, проведених з точки P до сторін трикутника ABC, є вершинами рівностороннього трикутника.

Розв'язок:

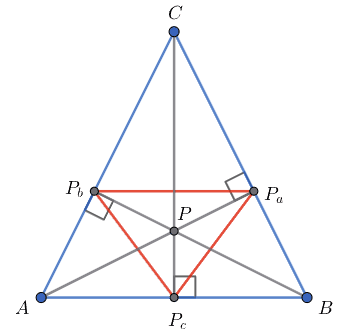
1. Позначимо через P_a, P_b і P_? основи перпендикулярів, проведених з точки P на сторони ΔABC. 

2. Сума кутів неопуклого чотирикутника APBC дорівнює 360°. Тому: ∠PAB + ∠APB + ∠BPC + ∠PCB + ∠CBA = 360°(1).  

3. Але ∠APB = ∠ACB + 60°; ∠BPC = ∠BAC +  60°. Підставляючи це в рівність (1) та враховуючи те, що ∠ACB + ∠BAC + ∠CBA = 180°, маємо 180° + ∠PAB + ∠PCB + 60° + 60° = 360°; а, отже, ∠PAB + ∠PCB = 60°.  

4. Якщо на AP як на діаметрі побудувати коло, то точки P_b і P_? лежатимуть на ньому (оскільки ∠AP_bP = ∠AP_cP = 90°). Тому ∠AP_bP_? = ∠PAP_c (як вписані кути, що спираються на ту саму дугу).  

5. Аналогічно ∠PP_bP_a = ∠PCP_a, бо точки P_b і P_a лежатимуть на колі діаметра PC.  

6. Маємо ∠P_aP_bP_c = ∠PP_bP_? + ∠PP_bP_a + ∠PAB + ∠PCB = 60°.  

7. Аналогічно доводимо, що ∠P_bP_aP_c = 60° і ∠P_aP_cP_b = 60°. Отже, ΔP_aP_bP_? – рівносторонній, що й треба було довести.