№ 6.44 Геометрія = № 14.44 Математика
Чотири магазини деякого підприємства розташовано у вершинах опуклого чотирикутника. Де йому слід розмістити товарний склад, щоб сума відстаней від складу до всіх магазинів була найменшою?
Розв'язок:
Чотири магазини деякого підприємства розташовано у вершинах опуклого чотирикутника. Де йому слід розмістити товарний склад, щоб сума відстаней від складу до всіх магазинів була найменшою?
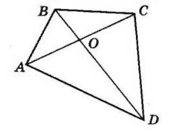
Нехай даний чотирикутник — ABCD, а O — деяка точка.
OA + OC ≥ AC за нерівністю трикутника,
при цьому OA + OC = AC в тому і тільки в тому випадку, коли O ∈ AC.
Аналогічно, OB + OD ≥ BD,
при цьому OB + OD = BD тоді і тільки тоді,
коли точка O лежить на діагоналі BD.
Отже, OA + OB + OC + OD ≥ AC + BD,
при цьому OA + OB + OC + OD = AC + BD тоді і тільки тоді,
коли точка O лежить одночасно на діагоналях AC і BD,
тобто є точкою перетину діагоналей чотирикутника ABCD.
Відповідь:
У точці перетину діагоналей чотирикутника.
