ВПР 1 №107 Алгебра = ВПТ 5 №34 Математика
Побудуйте графік функції:
1.$ \ y=\frac{30x-18x^2}{3x^3-5x^2};$
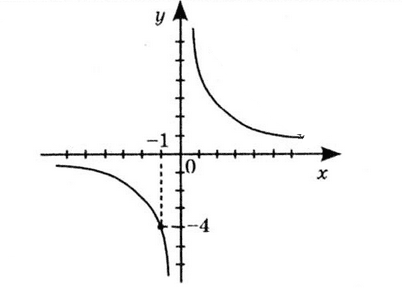
2. $\ y=\frac{4+x}{x^2+x}+\frac{3}{x+1}.$
Розв'язок:
1. $ \ y=\frac{30x-18x^2}{3x^3-5x^2}= \frac{6x\left(5-3x\right)}{x^2\left(3x-5\right)}=$
$= -\frac{6\left(3x-5\right)}{x\left(3x-5\right)}= -\frac{6}{x};$
D$\left(y\right) = x - будь-які,$
$ крім\ 0\ і\ \frac{5}{3}.$
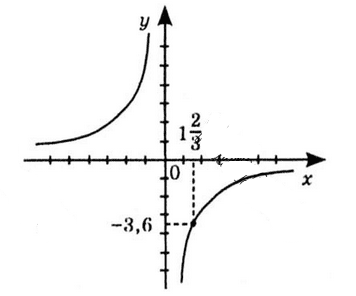
Якщо $x=\frac{5}{3}=1\frac{2}{3},$
то $y=-\frac{6}{5}=-\frac{18}{5}=$
$= -3\frac{3}{5} =-3{,}6.$
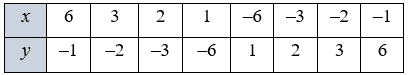
2. $\ y=\frac{4+x}{x^2+x}+\frac{3}{x+1}=$
$= \frac{4+x}{x\left(x+1\right)}+\frac{3}{x+1}=$
$= \frac{4+x+3x}{x\left(x+1\right)}=\frac{4+4x}{x\left(x+1\right)}=$
$= \frac{4\left(x+1\right)}{x\left(x+1\right)}=\frac{4}{x};$
D$\left(y\right) = x - будь-які,$
$ крім\ 0\ і -1.$